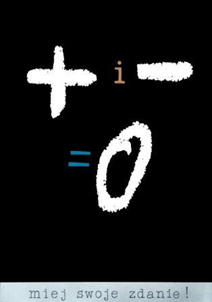
data publikacji: 15.07.2021
tekst: Janusz Maciaszek
„Obraz nie jest wart tysiąca słów”1 – napisał amerykański filozof Donald Davidson, kończąc artykuł poświęcony przyczynowej teorii metafory. Owo przyrównanie metafory do obrazu miało uzasadnić fakt, że nie ma czegoś takiego jak znaczenie metaforyczne, zaś to, co niesłusznie nazywamy parafrazą, jest jedynie opisem skutków oddziaływania metafory. Metafora ma tylko jedno znaczenie – znaczenie dosłowne, zaś jej przyczynowe oddziaływanie na psychikę słuchacza lub czytelnika bierze się z tego, że interpretacja dosłowna jest albo oczywistą prawdą, albo oczywistym fałszem, co wywołuje pewnego rodzaju dysonans poznawczy uruchamiający łańcuch przyczynowo-skutkowy prowadzący do jego zniwelowania.
Obraz nie jest tym samym co metafora językowa, chociaż – jak to jest w przypadku plakatu „Miej swoje zdanie!” – może zawierać explicite elementy językowe o potencjalnie metaforycznym charakterze. Zacznijmy od opisu plakatu w języku, który można by określić jako język „surowych faktów”. Na czarnym tle widać pięć symboli układających się na zarys formułki lub równania + i = 0, zaś na dole widnieje tytułowy napis „miej swoje zdanie!” Równanie nie zostało jednoznacznie podane, co stanowi zamierzoną niejednoznaczność. Wedle najprostszej – lecz nie jedynej – interpretacji byłoby to (+x) + (–x) = 0, bo spójnik „i” może pełnić funkcję naturalnojęzykowego odpowiednika operacji dodawania. Równanie to (a właściwie schemat równania) jest niekontrowersyjne, co w sposób oczywisty kontrastuje z podpisem. Jak bowiem można mieć własne zdanie w tak oczywistej sprawie?
W tym momencie zaczyna się – jak by to określił Davidson – opis skutków działania metafory. Owymi skutkami będą wszelkie akty psychiczne odbiorcy, które pojawiają się w procesie eliminowania dysonansu poznawczego związanego z absurdalnym przypuszczeniem, że Autor plakatu kwestionuje najprostsze prawa arytmetyki. Pozbycie się dysonansu poznawczego wymaga odwołanie się do szeroko rozumianego kontekstu, na który w tym przypadku składają się między innymi użyte kolory. Symbole składające się na równanie są jasne, zaś tło czarne. Matematyka jako wytwór rozumu jaśnieje na tle czarnej niewiedzy. Rozumu i jego wytwory konceptualizujemy bowiem jako jasność, blask, oświecenie lub „kaganek oświaty”. Niewiedzę jako ciemność (obskurantyzm) lub mrok (mroki średniowiecza). Są to bardzo typowe metafory pojęciowe, które przywołuję dlatego, że decydują o sposobie myślenia. Może zatem nie chodzi tu o kwestionowanie matematyki, lecz o to, czy znajomość matematyki, a w konsekwencji opartych na niej nauk ścisłych, jest w stanie rozświetlić mroki ludzkiej niewiedzy i odpowiedzieć na najistotniejsze dla człowieka pytania. Począwszy od Platona wielu filozofów uważało, że matematyka pełni funkcję królowej nauk, pozwalającej pozwala człowiekowi wyczytać wszystko, co jest istotne z „wielkiej księgi przyrody”. Aby tak było, rzeczywistość musiała być ze swej natury regularna i poznawalna, co stwarzało nadzieję, że to co jeszcze pozostaje ciemne może być z czasem oświetlone blaskiem rozumu. Przy tej interpretacji, tytułowe wezwanie do posiadania własnego zdania dotyczyłoby kwestii, czy nauka jest w stanie rozwiązać wszystkie istotne dla nas problemy, np. odwieczne pytanie o sens życia.
Przedstawiona tu interpretacja, chociaż nasunęła mi się jako pierwsza, nie wydaje się szczególnie ciekawa. Wręcz przeciwnie, grzeszy ona banalnością i przypomina szkolną analizę poezji romantycznej („mędrca szkiełko i oko”). Szukajmy więc dalej. Spójnik „i” może być również odpowiednikiem teoriomnogościowej operacji bycia częścią wspólną lub (przy nieco innej, lecz zbliżonej interpretacji) operatorem logicznym koniunkcji. Wtedy nasza formułka głosiłaby, że wspólna część zbioru obiektów posiadających pewną cechę oraz zbioru obiektów nieposiadających owej cechy jest zbiorem pustym lub – po prostu – że zdanie p i nie-p jest zdaniem logicznie fałszywe. Ponieważ w obu wersjach mamy do czynienia z niekwestionowaną oczywistością, tytułowe pytanie ponownie wywołuje dysonans poznawczy. Aby usunąć ów dysonans możemy nieco inaczej niż poprzednio zinterpretować czarne tło. Czerń nie musi bowiem jedynie reprezentować niewiedzę, ale również strach, pesymizm i obawy (czarny nastrój). Logika i teoria mnogości pozwalałyby nam te obawy rozwiać porządkując rzeczywistość tak, aby przestała być dla nas groźna.
Jako istoty używające języka mamy naturalną skłonność do kategoryzowania rzeczywistości, do odciskania na niej logicznych ze swej natury struktur językowych. Język pozwala „oswoić” rzeczywistość rozpraszając obawy i rozjaśniając myśli poprzez nałożenie na świat porządku narzucanego przez struktury języka porządku. Taka, w istocie pragmatyczna, interpretacja roli języka i logiki, którą określiłbym jako wersję light, nie jest szczególnie kontrowersyjna i zapewne nie usuwa dysonansu poznawczego związanego z tytułem. Być może zatem chodzi tu o inny rodzaj „porządkowania rzeczywistości” – a mianowicie o przekonanie, że rzeczywistość „sama przez się” ma logiczną strukturę. Za taki pogląd (nazwę go wersją hard) trzeba jednak zapłacić bardzo wysoką cenę, należy bowiem – jak to uczynił Arystoteles w Kategoriach – podzielić rzeczywistość na wzajemnie wykluczające się gatunki i rodzaje zakładając tym samym izomorfizm myśli, języka i rzeczywistości (nieco inaczej zrobił to w Traktacie Ludwig Wittgenstein). Aby bez ograniczeń korzystać z dobrodziejstw logiki trzeba założyć, że rzeczywistość jest zero-jedynkowa. Wezwanie „miej swoje zdanie!” może zatem być apelem o zakwestionowanie tego poglądu.
Wydawać by się mogło, że powyższa interpretacja jest wydumana i nie dotyczy – jak napisał ongiś Frege – ludzi nietkniętych filozofią. Nic bardziej mylnego. Przekonanie o zero-jedynkowości świata jest stanowiskiem całkowicie naturalnym dla większości ludzi. Pozwolę sobie na przytoczenie wyrazistego przykładu, chociaż sprawa jest bardziej ogólna. Znany jest upór pewnych środowisk, aby odmawiać istnienia osobom LGBT. Oczywiście nie chodzi o to, że ktokolwiek utrzymuje, że osób takich nie ma, lecz o to, że osoby te faktycznie są albo kobietami, albo mężczyznami, zaś określanie przez nich samych siebie jako osoby LGBT jest jedynie fałszywym stanem świadomości spowodowanym przez bliżej niesprecyzowaną, lecz groźną ideologię. W tym kontekście staje się jasne stwierdzenie, że LGBT to nie ludzie, ale jedynie ideologia. Przekonanie o dychotomicznym podziale ludzi na kobiety i mężczyzn (co dodatkowo wsparte jest znanym cytatem biblijnym) ma – w mniemaniu żywiących je osób – być konsekwencją panującego w rzeczywistości porządku i ładu. Są tylko kobiety i tylko mężczyźni, każde z nich (wbrew zgubnej ideologii gender) ze ściśle przypisanymi do swojej płci rolami społecznymi. Mamy pełny porządek i przewidywalność – świat jest prosty i bezpieczny, a tylko niektórzy wprowadzają weń zamieszanie mącąc młodzieży w głowach. Intencje osób głoszących pogląd o logicznej strukturze świata zapewne są dobre (bo kto ma złe zamiary?), ale konsekwencje utrzymywania takiego stanowiska nie zawsze są pożądane. Tendencja do dzielenia świata na ostre i wykluczające się wzajemnie zbiory jest powszechna. Taki świat może wprawdzie wydawać się bezpieczniejszy, ale kosztem tego, że przestaje być zniuansowany. Na plakacie reprezentuje to kontrast między czernią tła i jasnymi kolorami formuły. Logika ma wyeliminować strach i niepewność, usuwając to co czarne, gdyż po stronie bytu nie ma dla niego miejsca. Jeżeli jednak uznamy, że rzeczywistość nie jest w pełni zero-jedynkowa, to znajdzie się w niej miejsce zarówno dla logiki, jak i dla strefy cienia. Nie będzie jednak ona czarna, lecz będzie przybierała różne odcienie i kolory. Rzeczywistość pozbawiona logicznej struktury nie musi być zatem przerażająca i być może nie należy obawiać się tego co niedookreślone, a przez to nieprzewidywalne. Gdyby tak rozumieć wezwanie „miej swoje zdanie!”, to byłoby to wezwanie do zaakceptowania istnienia strefy cienia (nie czerni!), nieostrości oraz do rezygnacji ze – związanego z wiarą w logiczną strukturę świata – złudnego poczucia komfortu.
Zobacz inne plakaty Zbigniewa Waszczeniuka
"Zgadza się" nie znaczy "zgodnie", 1974
Pan Fajnacki, 1986
1 Donald Davidson, What Metaphors Mean, w: tegoż, Inquiries into Truth and Interpretation, Claredon Press, Oxford 2001, s. 263.
